A KG-GNN-LLM Framework for Latent Space Context Synthesis

Introduction

In recent years, large language models (LLMs) have displayed extraordinary capabilities across a range of natural language processing tasks, including question answering (QA), text summarization, and conversation modeling. These models, trained on massive corpora of unstructured text, often excel at generating fluent, coherent responses. However, when faced with queries that require complex reasoning, domain-specific understanding, or factual grounding outside their training distribution, LLMs frequently exhibit limitations such as hallucinations, superficial reasoning, and inaccuracies. As the complexity of user queries and domains continues to increase—spanning specialized fields like biomedicine, finance, and scientific literature—there is a growing need for methodologies that can augment LLMs with reliable, context-rich, external knowledge sources.

Knowledge graphs (KGs) offer a structured representation of entities and their relationships, capturing intricate semantic links that go beyond the linear narrative found in unstructured text. By encoding real-world facts and domain-specific information as graph-structured data, KGs provide a natural substrate for advanced reasoning. Despite their potential, integrating KGs into LLM workflows remains challenging. Conventional retrieval-augmented generation (RAG) approaches rely on appending retrieved text documents to the LLM’s input, which can supply facts but not the relational structure inherent in a knowledge graph. Directly bridging the latent space of language models with the structured embeddings of a knowledge graph presents an open research question: How can we inject KG-derived embeddings into an LLM in a way that improves factual grounding, leverages relational information, and preserves the model’s existing linguistic capabilities?

Recent advances in graph representation learning—particularly the success of Graph Neural Networks (GNNs), such as Graph Convolutional Networks (GCNs), Graph Attention Networks (GATs), and GraphSAGE—provide a pathway to encoding and refining node representations that incorporate the topological and semantic structure of KGs. GNNs translate graph connectivity patterns and node attributes into vector embeddings, making it possible to align structured graph knowledge with the linguistic representations in LLMs. However, many existing methods either fine-tune the LLM parameters jointly with graph embeddings or rely on intricate pipelines that compromise the original model’s training distribution.

In this work, we propose a method that integrates GNN-derived embeddings from a knowledge graph into a frozen LLM, specifically a pretrained GPT-2 model. Instead of altering the LLM’s parameters, we treat the GNN and the KG as an adaptable external knowledge engine. For each question-answering scenario, we compute embeddings for both the candidate answers and the relevant node representations from the KG. By selecting and injecting the most appropriate graph-derived embedding directly into GPT-2’s input context, we introduce a latent hint that guides the LLM toward more grounded and contextually consistent predictions.

We evaluate our approach on multiple datasets, including BioGraph—a large, diverse graph sourced from academic literature—and MetaQA, a smaller, domain-specific movie ontology. Our experiments show that GNN-based embeddings integrated into a frozen LLM can significantly improve validation performance on multiple-choice QA tasks. Moreover, the choice of GNN architecture matters: GraphSAGE excels in the larger, sparser BioGraph, while GCN and GAT outperform GraphSAGE on the more structured, domain-specific MetaQA dataset. This variation underscores the importance of tailoring graph representation methods to the nature of the underlying knowledge graph.

Key Novelty

Unlike previous approaches that fine-tune or heavily modify the LLM, our method introduces a simple, direct mechanism for injecting GNN-derived embeddings into a frozen LLM’s latent space. By using a single special token replaced with a GNN-generated embedding, we preserve the integrity of the pretrained language model while enabling it to leverage external graph structure and domain-specific information with minimal overhead, creating a modular and flexible framework for integrating external knowledge.

Related Works

A central challenge in natural language processing (NLP) is enabling large language models (LLMs) to handle queries that demand factual correctness, domain specificity, and nuanced reasoning. Traditional LLMs, trained purely on unstructured text, often struggle with these requirements, leading to hallucinations and inaccuracies, especially when dealing with intricate, domain-specific queries [12,13]. This limitation motivates research into augmenting LLMs with structured sources of external knowledge, such as knowledge bases and knowledge graphs, which can supply factual grounding and relational context not readily captured by statistical language modeling alone.

One widely explored direction involves retrieval-augmented generation (RAG), where external textual documents or database entries are retrieved and appended to the model’s input [14,15]. While RAG approaches have demonstrated improvements in factual consistency over pure LLMs, they primarily rely on ad-hoc textual snippets, lacking an explicit encoding of relational structure. This hinders their ability to deeply model the connections between entities, a critical aspect for complex reasoning and inference tasks. As a result, purely textual retrieval may still fail to exploit the full extent of semantic relationships, especially in dense or highly interconnected knowledge domains.

Integrating knowledge graphs (KGs) directly into LLMs offers an appealing solution to this structural gap. KGs represent information as a network of entities (nodes) linked by relations (edges), providing a richly structured semantic space. Prior work on knowledge-grounded language models has shown that incorporating KG embeddings into transformer-based architectures can yield more accurate and explainable predictions, especially in tasks like QA, entity disambiguation, and semantic retrieval [10,11]. However, a persistent challenge is how to effectively merge the rich, relational representations from KGs with the latent space representations learned by LLMs, without compromising the models’ pre-learned linguistic capabilities.

Graph Neural Networks (GNNs), including Graph Convolutional Networks (GCNs) [2], Graph Attention Networks (GATs) [4], and GraphSAGE [5], have emerged as powerful tools for encoding the structural properties of graphs. Their success spans numerous domains, from social network analysis and recommendation systems to biomedical applications and knowledge graph completion [19,20]. Yet, while GNNs have been integrated into end-to-end pipelines with language models, a major limitation remains: previous methods often rely on either fine-tuning the LLM alongside the GNN or painstakingly engineering complex interfaces between the two components [21,22]. This can be computationally expensive and can potentially distort the LLM’s pretrained distribution.

Our work builds on these ideas by proposing a direct, “freeze-and-insert” paradigm. We do not fine-tune the LLM; instead, we train the GNN component to produce embeddings that fit seamlessly into the LLM’s latent space. This approach builds on insights from representation learning literature, where general tranformations (linear or nonlinear) operations on embeddings often reflect meaningful semantic transformations [17,16]. Previous research has shown that latent space arithmetic can be applied to prompts, word embeddings, and even multimodal representations [16,18]. By leveraging this property, we directly insert GNN-derived embeddings (corresponding to knowledge-graph entities and relations) into the model’s input, allowing the LLM to benefit from structured knowledge without altering its internal parameters.

In doing so, we address the need for a method that integrates external graph structure into LLM reasoning without necessitating extensive joint training or fine-tuning. Prior studies have either focused on textual retrieval (RAG) approaches lacking structural insight [14,15] or on KG-based methods that require additional complexity and retraining of the language model [21]. Our contribution is to demonstrate a lightweight mechanism for injecting GNN-refined, KG-derived embeddings into a frozen LLM. This method stands to enhance domain-specific reasoning and factual correctness—two key limitations noted in earlier research—by providing a structured, semantically enriched latent representation that the LLM can utilize for better informed answer selection.

Methods

We propose a method to integrate external knowledge from a domain-specific knowledge graph into a large language model (LLM) inference for multiple-choice question answering (QA). This approach employs a pretrained GPT-2 model [1] as a text encoder and a Graph Neural Network (GNN) to refine node embeddings from the knowledge graph. The node features are transformed from text into a token llm, formed by taking the sequence dimension mean of the last layer of GPT-2. By incorporating graph-derived embeddings into GPT-2 prompts, we guide the language model toward knowledge-consistent answers without fine-tuning GPT-2 itself. We train the system as a whole, where the LLM weights are frozen, using its cross entropy loss as a signal for updating the GNN parameters. Figure 1 illustrates the model architecture.

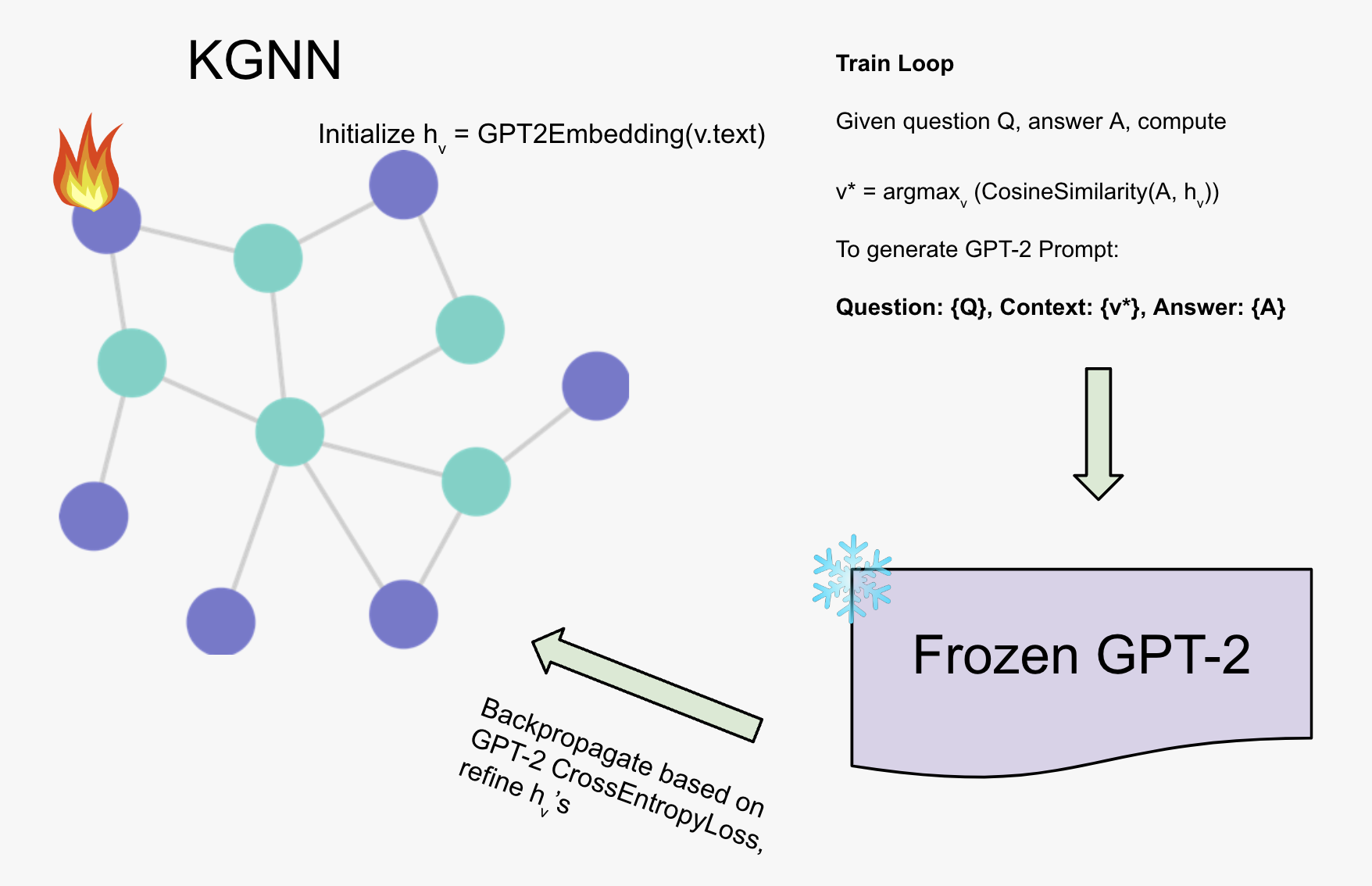
Dataset Characteristics

We conduct our experiments on two datasets: BioGraph, a knowledge graph assembled from academic papers, and MetaQA, a smaller movie-ontology dataset [7]. Table 1 summarizes key structural properties of both datasets.

The BioGraph dataset is provided as a pre-defined GraphML file, which includes a train and validation split of question-answer pairs referencing nodes in the graph. We load this GraphML file using NetworkX and extract node-level textual descriptors for each entity. For MetaQA, the input format is a list of triple-based facts provided in a plain text file. We parse this file to construct the corresponding graph structure, ensuring consistency with the BioGraph processing pipeline.

Knowledge Graph Embeddings

We start with a domain-specific knowledge graph stored in GraphML format, encoding entities as nodes and their relationships as edges. The graph is loaded using NetworkX [3]. Each node \((i)\) has a textual descriptor \((T_i)\). We tokenize \((T_i)\) and obtain token-level representations from GPT-2’s final-layer hidden states. By averaging this embedding along the sequence dimension, we form the initial node embedding:

$$ h_i = \text{mean}_{t \in T_i} \text{GPT2}(t) $$

This process yields a semantic representation for each node, derived purely from GPT-2’s pretrained language modeling capabilities. GPT-2 parameters remain frozen to preserve the knowledge learned during pretraining.

Graph Neural Network Architectures

After obtaining initial node embeddings \(\{h_i\}\), we consider three GNN architectures to incorporate graph structure: Graph Convolutional Networks (GCN) [2], Graph Attention Networks (GAT) [4], and GraphSAGE [5]. We apply each GNN to the initial embeddings and compare their downstream validation loss.

Graph Convolutional Network

Let \((A)\) be the adjacency matrix of the graph (with self-loops) and \((D)\) the corresponding degree matrix. We initialize \((X^{(0)} = [h_1; h_2; \ldots; h_N])\). A two-layer GCN transforms node features as follows:

$$ X^{(1)} = \sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} X^{(0)}W^{(0)}), \quad X^{(2)} = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} X^{(1)}W^{(1)} $$

Here, \(\tilde{A} = A + I\) and \(\tilde{D}\) is the degree matrix of \(\tilde{A}\). The matrices \((W^{(l)})\) are learnable parameters, and \(\sigma\) is a ReLU activation function. This process produces refined embeddings \((X^{(2)} = [g_1; g_2; \ldots; g_N])\), where each \((g_i)\) encodes the semantic information of node \((i)\) along with its local graph structure.

Graph Attention Network

Graph Attention Networks (GAT) [4] introduces self-attention mechanisms to graph node feature aggregation. Instead of uniformly averaging neighbor information, GAT computes attention coefficients:

$$ \alpha_{ij} = \frac{\exp(\text{LeakyReLU}(a^\top [W^{(0)}h_i \parallel W^{(0)}h_j]))}{\sum_{k \in \mathcal{N}(i)} \exp(\text{LeakyReLU}(a^\top [W^{(0)}h_i \parallel W^{(0)}h_k]))} $$

Here, \(\mathcal{N}(i)\) denotes the neighbors of node \(i\), \(\parallel\) denotes concatenation, \(W^{(0)}\) and \(a\) are learnable parameters. By using multiple attention heads and averaging their outputs, GAT refines node embeddings according to the relevance of each neighbor.

$$ X^{(1)} = \big\Vert_{m=1}^M \sigma\left(\sum_{j \in \mathcal{N}(i)} \alpha_{ij}^{(m)} W^{(0)}h_j\right) $$

Applying another GAT layer similarly yields \(X^{(2)}\), producing attention-enhanced node embeddings.

GraphSAGE

GraphSAGE [5] learns an aggregator function to sample and aggregate neighbor information, enabling inductive node embedding generation for large graphs. A typical GraphSAGE layer updates:

$$ h_i^{(1)} = \sigma\big(W^{(0)} [h_i^{(0)} \parallel \text{AGG}(\{h_j^{(0)}: j \in \mathcal{N}(i)\})]\big) $$

where \(\text{AGG}\) can be a mean, LSTM-based, or pooling aggregator. For our experiments, we use a mean aggregator. After a second layer:

$$ h_i^{(2)} = \sigma\big(W^{(1)} [h_i^{(1)} \parallel \text{AGG}(\{h_j^{(1)}: j \in \mathcal{N}(i)\})]\big), $$

we obtain \((X^{(2)} = [g_1; g_2; \ldots; g_N])\) with GraphSAGE-specific embedding structure.

Integrating Graph Embeddings into the Language Model

Consider a multiple-choice QA scenario with a question \((Q)\) and candidate answers \(\{A_1, A_2, \ldots, A_k\}\). For each answer \((A_j)\), we compute:

$$ a_j = \text{mean}_{t \in A_j} \text{GPT2}(t) $$

We then find the node whose refined embedding \((g_{n_j})\) is most similar to \((a_j)\), using cosine similarity:

$$ n_j = \arg\max_i \frac{a_j^\top g_i}{\|a_j\|\|g_i\|} $$

The selected node embedding \((g_{n_j})\) is inserted into GPT-2’s context. We introduce a special token \(\langle\text{graph}\rangle\) into the model’s prompt:

"Question: \((Q)\)
Context: \(\langle\text{graph}\rangle\)
Answer: \((A_j)\)"

GPT-2 uses its pretrained embeddings for all text except \(\langle\text{graph}\rangle\), which we replace with \((g_{n_j})\). Thus, GPT-2 is conditioned on a graph-derived embedding that provides external contextual knowledge. By keeping GPT-2 frozen, we rely on the GNN to learn representations that are directly useful for improving answer selection.

Training and Objective

We train only the GNN parameters (whether GCN, GAT, or GraphSAGE) by maximizing the likelihood of the correct answer. For each training example \((Q, A_{\text{correct}})\):

$$ \mathcal{L}(\theta) = -\sum_{(Q,A_{\text{correct}})} \log p_\theta(A_{\text{correct}} | Q, g_{n_{\text{correct}}}) $$

Here, \((p_\theta)\) is the probability assigned by GPT-2 when the graph embedding is inserted. GPT-2 remains fixed, and \(\theta\) (the GNN parameters) are updated to yield node embeddings that help GPT-2 choose the correct answer more confidently.

Experimental Setup

All models and training procedures are implemented in PyTorch [8], with GPT-2 integrated using HuggingFace Transformers [9]. GCN, GAT, and GraphSAGE layers are implemented using PyTorch Geometric [10], and NetworkX [3] handles graph loading. By comparing how the validation loss evolves for each GNN-based method on BioGraph and MetaQA, we aim to glean insights into the efficacy of graph-based embeddings for knowledge-consistent QA. We use AdamW [6] for optimization, tuning hyperparameters (e.g., hidden dimensions, learning rates) based on validation performance.

Results

Hyperparameter Validation

Before finalizing our model configurations, we performed a series of validation experiments (all on the BioGraph dataset, due to compute limits) to determine appropriate hyperparameters for each of the GNN architectures (GCN, GAT, and GraphSAGE). We conducted controlled searches over hidden dimension sizes and neighbor sampling rates (for GraphSAGE) on the validation sets of our datasets.

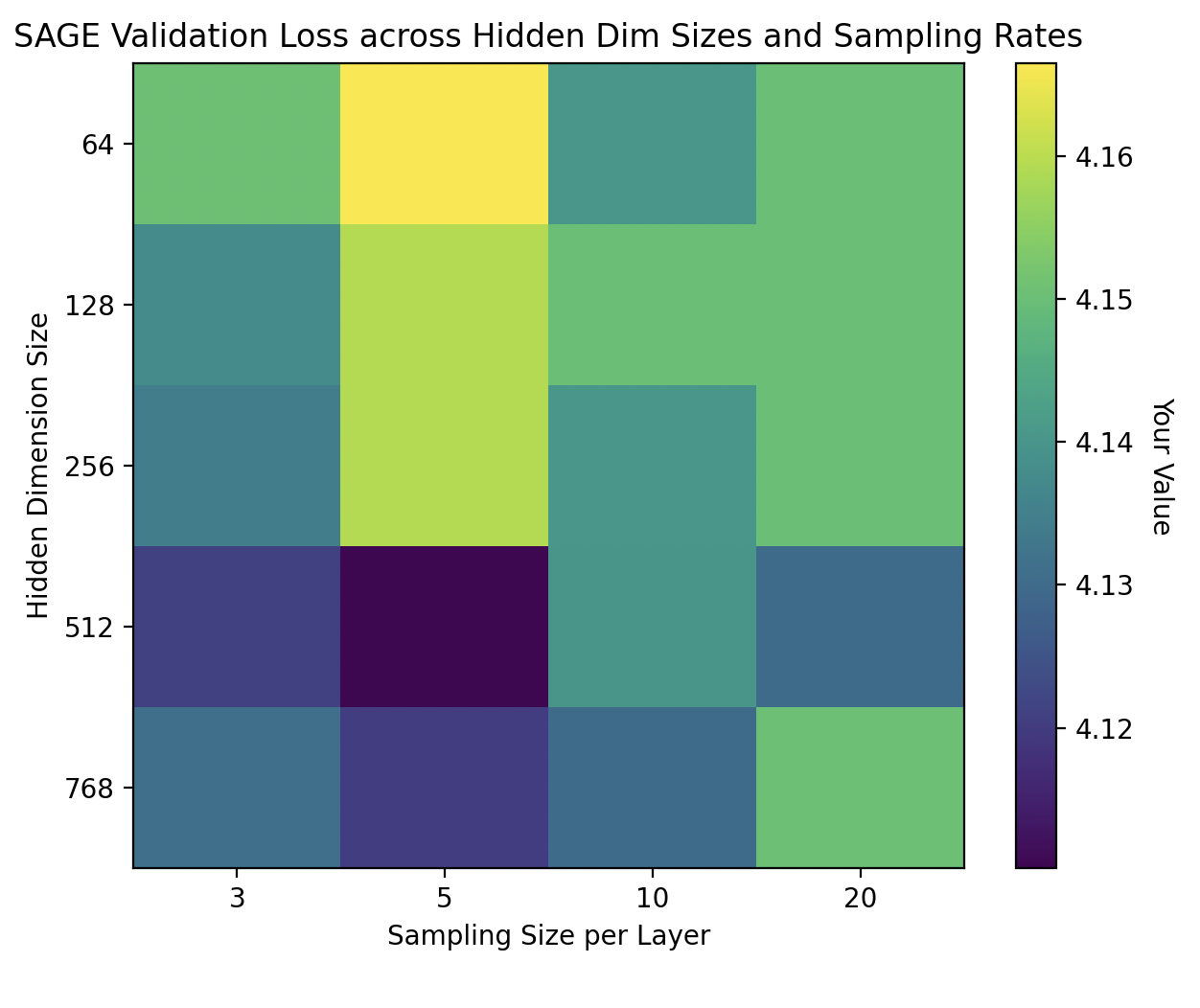
For GraphSAGE, we experimented with hidden dimensions from \(\{64,128,256,512,768\}\) and sampling sizes per layer from \(\{3,5,10,20\}\). As shown in the heatmap below, the optimal configuration for GraphSAGE emerged at a hidden dimension of 512 and a sampling size of 5 neighbors, yielding notably improved validation loss on our validation sets:

For GCN and GAT, we varied the hidden dimensions in the same set \(\{64,128,256,512,768\}\). The validation results revealed that a 512-dimensional hidden layer was also effective for these architectures:

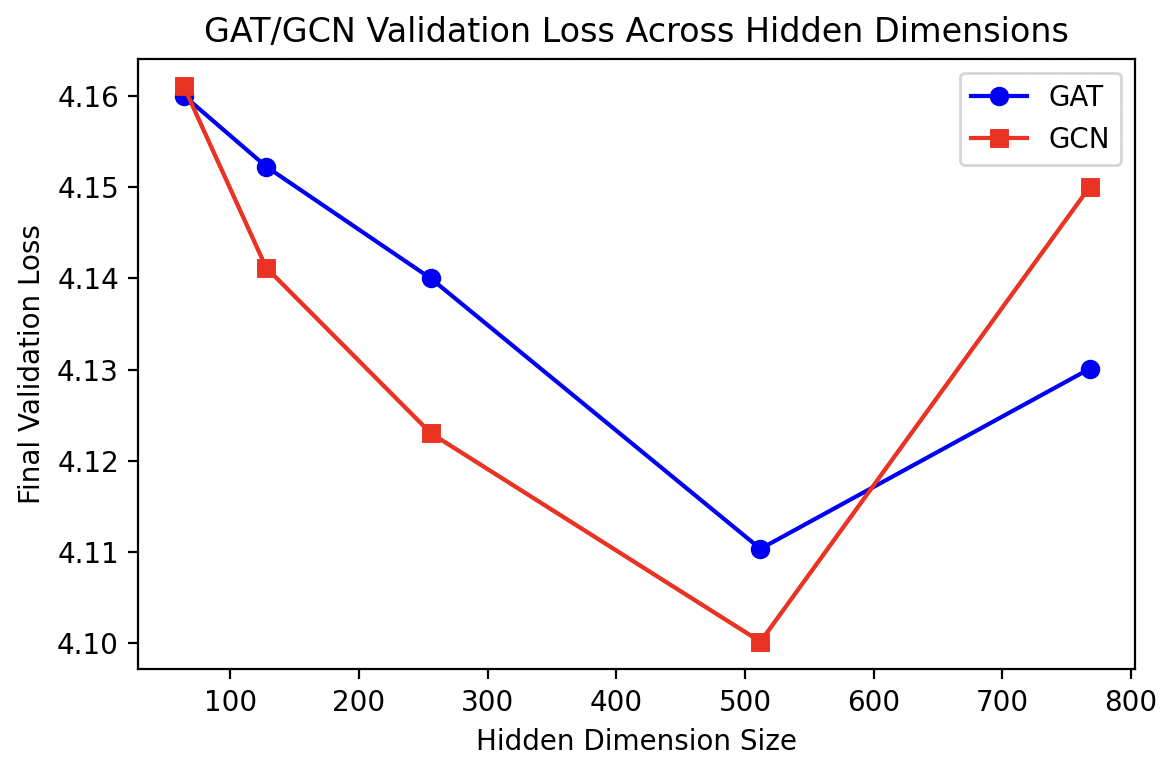
Equipped with these optimized hyperparameters (hidden dimension = 512 for all GNNs and sampling size = 5 neighbors for GraphSAGE), we proceed to evaluate these configurations on both BioGraph and MetaQA datasets.

Performance on BioGraph

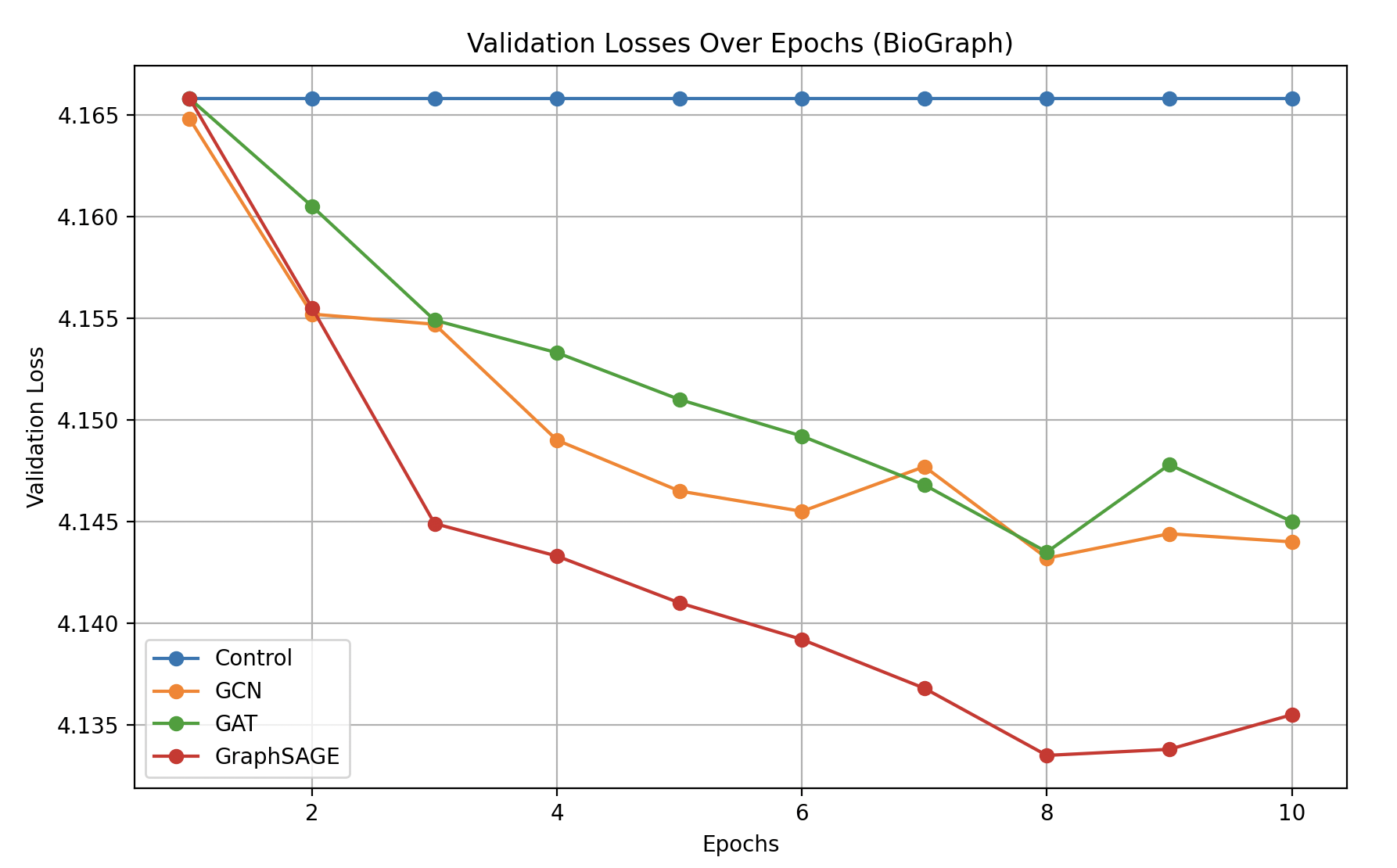
On the BioGraph dataset, integrating graph-derived embeddings into GPT-2 reduces validation loss relative to the control (no GNN) condition. While GCN and GAT yield improvements, GraphSAGE shows the most pronounced reduction in validation loss over epochs. The figure below illustrates how GraphSAGE steadily outperforms both GCN and GAT on this larger, more heterogeneous knowledge graph.

Performance on MetaQA

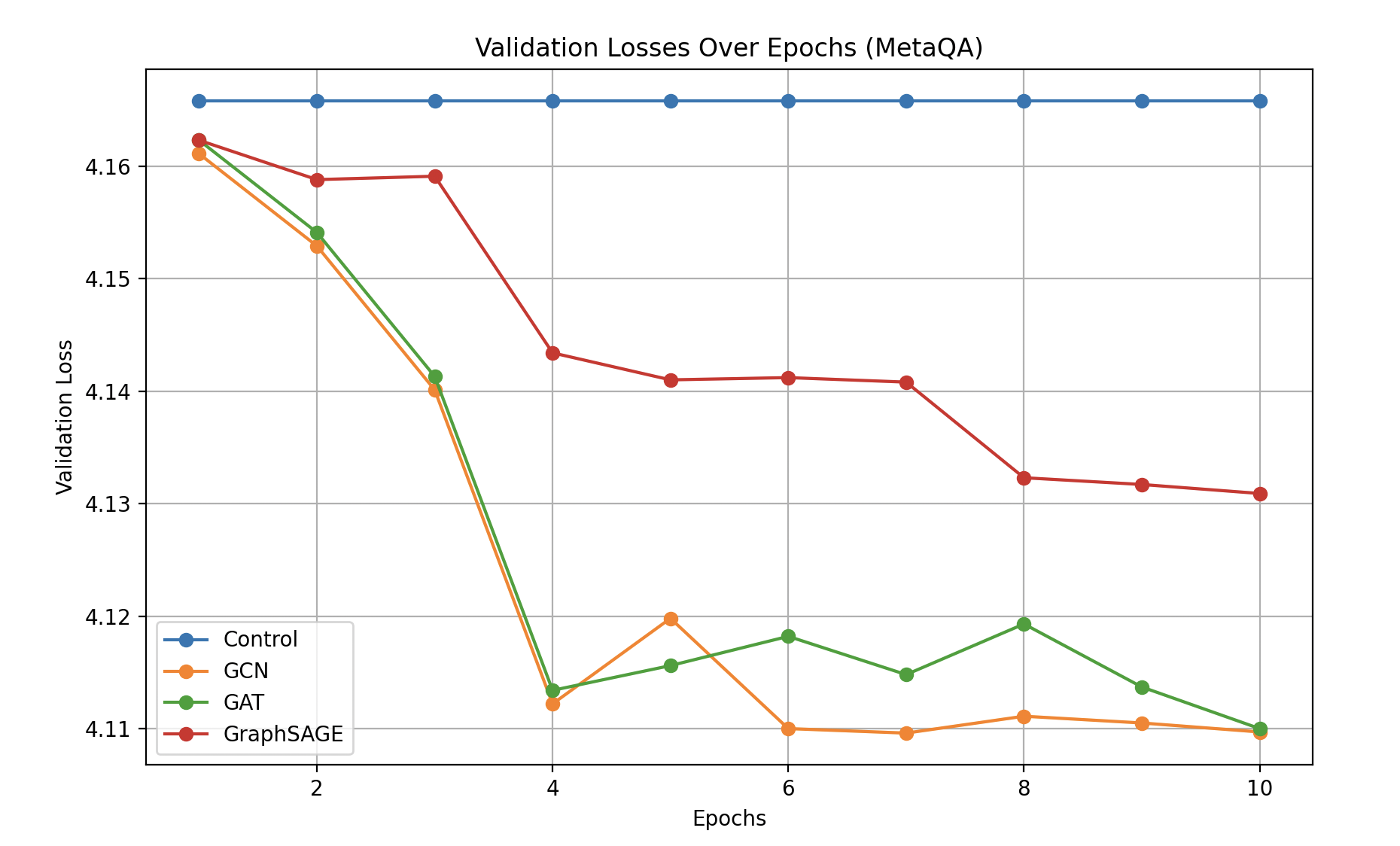
On the smaller MetaQA dataset, all GNN-based methods again outperform the control, confirming that integrating external graph structure is beneficial. However, the relative order of model performance differs from the BioGraph results. Here, GCN and GAT achieve lower validation losses than GraphSAGE, suggesting that the nature of the knowledge graph and its complexity influences which GNN architecture yields the greatest benefit.

The results suggest that while GraphSAGE’s sampling-based approach excels on the larger BioGraph dataset, GCN and GAT might be better suited to MetaQA’s characteristics (e.g., density, connectivity patterns, or domain-specific structure). This highlights that no single GNN architecture universally dominates; performance depends on graph properties and the underlying domain.

Summary of Findings

Our experiments demonstrate that integrating GNN-based embeddings into GPT-2 improves multiple-choice QA performance over a no-graph-control across both BioGraph and MetaQA datasets. However, the best-performing GNN architecture depends on the dataset. On BioGraph, GraphSAGE emerges as the strongest performer, while on MetaQA, GCN and GAT offer superior results.

These observations underscore the importance of selecting and tuning GNN architectures based on dataset characteristics. While 512-dimensional embeddings were generally effective, and GraphSAGE benefited from a sampling size of 5 neighbors, the optimal configuration is task-dependent. Future work may explore more nuanced architectural choices or adaptive approaches that consider graph structure and domain constraints when selecting a GNN.

Discussion

The findings of our study underscore the potential of integrating structured graph-based representations into pretrained language models to improve factual grounding in multiple-choice QA tasks. By leveraging embeddings produced by GNNs—specifically GCN, GAT, and GraphSAGE—and injecting them into GPT-2’s context, we have demonstrated that knowledge graph information can guide a language model towards more informed and contextually relevant answer selection, all while keeping the language model itself frozen.

One key observation emerging from our experiments is the dependency of performance on the characteristics of the underlying knowledge graph and the chosen GNN architecture. Our results show that on BioGraph, a large, heterogeneous graph containing interdisciplinary and sparsely related academic knowledge, GraphSAGE outperformed the other GNN architectures. GraphSAGE was developed with the explicit goal of handling inductive learning settings and efficiently sampling neighborhoods in large graphs. Its success on BioGraph could be attributed to its ability to draw richer, more representative samples from highly varied node neighborhoods. In more complex or less densely connected graphs, adaptive sampling strategies may help retain the most pertinent relational signals. The improved performance of GraphSAGE on BioGraph therefore highlights the importance of carefully considering the nature of the graph and tailoring the GNN choice to its structural properties.

Conversely, on MetaQA—a smaller, more domain-specific dataset focused on movie knowledge—GCN and GAT methods surpassed GraphSAGE. The simpler connectivity patterns and domain-specific ontology of MetaQA may have made standard aggregations (GCN) or attention mechanisms (GAT) more effective. In this environment, sampling strategies may have introduced unnecessary variance or complexity, whereas methods that rely on attentive or uniform aggregation across the entire neighborhood provided more stable and direct representations. This contrast between the two datasets suggests that no single GNN architecture universally outperforms the rest; rather, the “best” GNN often depends on the graph’s density, domain-specificity, and connectivity patterns.

Another important observation is that the improvements in validation loss were more pronounced on the MetaQA dataset. MetaQA’s more cohesive and narrowly scoped domain may offer fewer ambiguous relations, allowing the GNN-augmented language model to more easily form accurate representations. In contrast, BioGraph’s heterogeneous nature introduces complexity that can dilute the immediate impact of graph-derived signals, resulting in more modest, though still valuable, performance gains. This finding underscores the value of domain specificity: more narrowly defined domains, with more coherent and consistent node-to-node relationships, can lead to more substantial improvements when integrating graph embeddings.

While our study demonstrates that integrating GNN embeddings into GPT-2’s prompts can guide the model toward better answer selection, it should be noted that GPT-2 is a relatively small and outdated language model by current standards. This project serves as a proof of concept, illustrating the potential of directly injecting learned node embeddings into a language model’s input stream. Future work should explore more powerful models such as GPT-4 or other state-of-the-art LLMs. With more computational resources and larger models, it may be possible not only to see greater improvements in accuracy and factual grounding but also to rigorously evaluate downstream QA performance, rather than relying solely on validation loss. Moreover, adopting more diverse and sophisticated GNN architectures—or even architectures that dynamically adapt their processing strategy based on the graph’s characteristics—could yield further gains. Temporal or multimodal graphs, where nodes and edges evolve over time or incorporate signals from images, audio, or structured databases, represent another promising avenue for extension.

In sum, our results point toward a research direction where structured knowledge, represented via tailored GNN embeddings, can enhance LLM capabilities without requiring expensive finetuning. As graph data and language models continue to evolve, the synergy between these domains holds the potential to advance our ability to answer complex questions, reduce hallucinations, and ultimately enrich the knowledge integration process in AI-driven information retrieval and decision-making.